백트래킹이란?
백트래킹은 해를 찾는 과정에서 여러 가능성을 탐색하다가, 특정 경로가 잘못되었음을 알게 되면 되돌아가서 다른 경로를 시도하는 문제 해결 기법이다. 모든 가능한 경우의 수를 탐색하지만, 가지치기(pruning)를 통해 비효율적인 경로를 배제하여 효율성을 높인다. 다시 말해, 완전 탐색(브루트 포스)의 개선된 형태라 할 수 있다.
단순히 요약하자면, 백트래킹은 "이 길이 아닌 것 같을 때 원래 왔던 길로 되돌아가서 다른 길을 가보는 것"이다. 이는 특성으로 알 수 있듯이 대부분 DFS로 구현할 수 있다.
백트래킹의 예시
이번 예시는 9663번 N-Queen 문제를 기준으로 하겠다.
먼저 구현 문제를 보자.
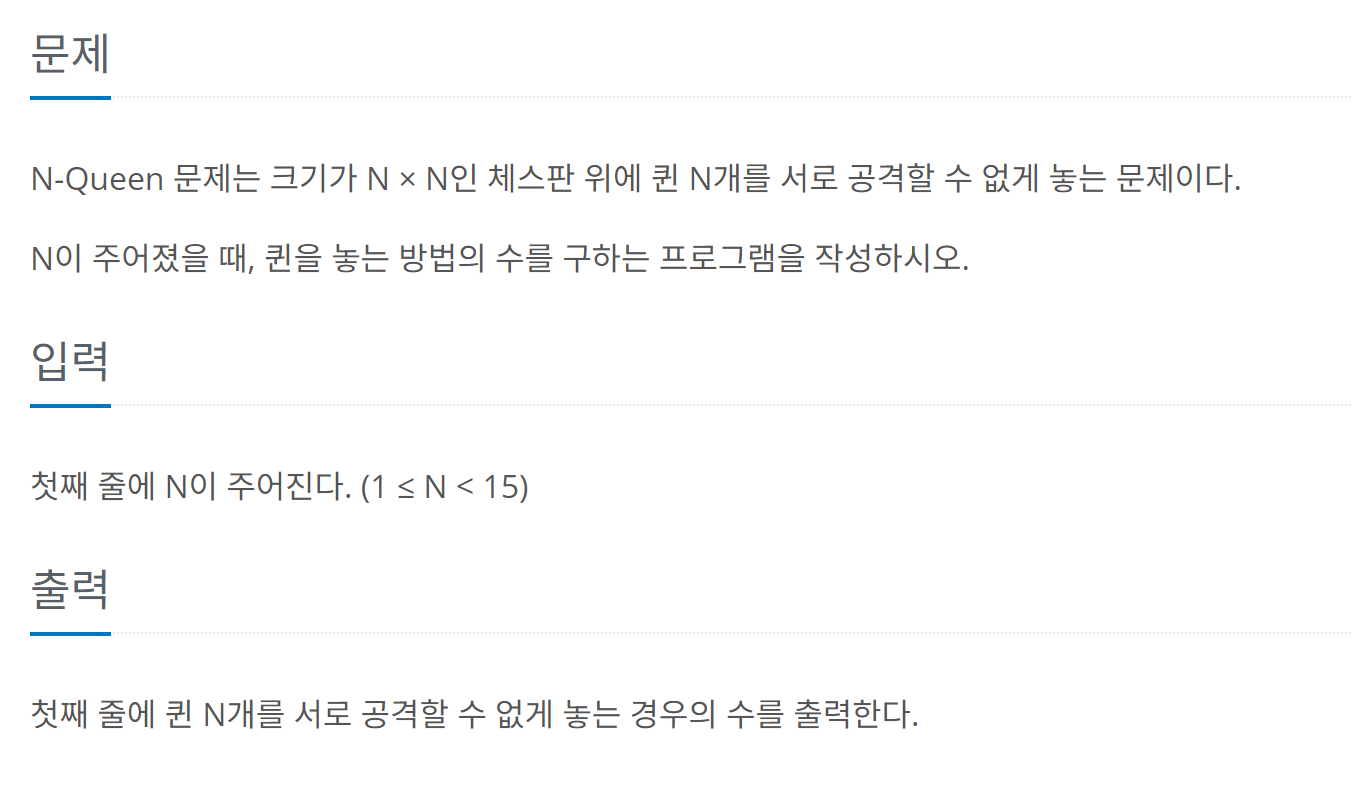
문제 자체는 백트래킹을 잘 활용해야 풀 수 있다. 나는 문제를 다 읽고 2차원 배열로 풀었는데 이후 풀이를 찾아보니 이게 웬걸... 1차원 배열로 더 짧은 시간에 효율적인 풀이가 있었다. 신박해서 굉장히 놀라웠다. 겸손한 자세로 앞으로도 정진해야겠다..
본론으로 와서 신박하고 효율적인 다음 풀이를 보자.
public class N퀸 {
static int n;
static int[] arr;
static int cnt = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
n = Integer.parseInt(br.readLine());
arr = new int[n];
dfs(0);
bw.write(cnt + "\n");
bw.flush();
bw.close();
}
static void dfs(int depth) {
if (depth == n) { // 1
cnt++;
return;
}
for (int i = 0; i < n; i++) { // 2
arr[depth] = i;
if (isPossible(depth)) { // 3
dfs(depth + 1); // 4
}
}
}
static boolean isPossible(int col) {
for (int i = 0; i < col; i++) {
if (arr[col] == arr[i]) { //3-1
return false;
}
else if (Math.abs(col - i) == Math.abs(arr[col] - arr[i])) { // 3-2
return false;
}
}
return true;
}
}
이 풀이에서는 배열의 index를 열, 각 index의 값을 행이라고 가정했다.
- 재귀를 종료하는 조건은 depth가 n번일 때다. n을 4라고 했을 때 재귀를 진행하다가 depth가 4가 되면 종료하도록 조건을 달았다.
- 해당 열(depth)에 i번째 행에 퀸을 놓을 수 있는지 n번째까지 검사한다.
- 2번의 검사는 이 isPossible 메소드에서 진행한다.
- 해당 열의 행(depth, col)과 i번째 열의 행이 동일할 경우, 다시 말해 같은 행에 있을 경우, 불가능이라 판단하여 false를 반환한다.
- 이 부분이 가장 이해하기 어려웠지만 시간을 들이니 이해가 됐다. 아래 예시를 보자. 예를 들어, 퀸들이 각각 (0,0)과 (1,1)에 있다면, 다음과 같은 계산이 된다.
- col - i = 1 - 0 = 1
- arr[col] - arr[i] = 1 - 0 = 1 따라서 열과 행의 차이가 같으므로 대각선에 있다고 여길 수 있다.
- 여기서도 의문일 수 있다. 왜 abs를 사용했는가? 이 또한 어렵지 않다. 아래 예시를 보면 0번째과 1번째 열에서 퀸의 행 위치를 이용해 행의 차를 계산했을 때 음수가 나올 수도 있다. 위처럼 (0,0)과 (1,1)에 퀸이 위치해있다면 음수가 나올 것이기에 이는 앞선 열의 차로 인해 대각선이라는 것을 알아도 실제론 대각선이 아니라고 나오기 때문이다.
- 해당 열의 행에 놓을 수 있다면 다음 재귀함수를 호출한다. 이는 다음 열에 놓을 위치 찾기를 시작하는 것과 같다.
0 1 2 3
0 Q - - -
1 - - Q -
2 - - - -
3 - Q - -
내가 생각한 풀이와 너무 다른데다 굉장히 짧고 효율적이어서 처음 보자마자 이게 어떻게 돌아가는지 이해할 수 없었다. 그러나 규칙을 보면 이해하지 못할 건 아니었다. 아래 그림처럼 결국 다음 열의 행에서만 놓을 수 있는 곳 찾으면 되는 것이다.
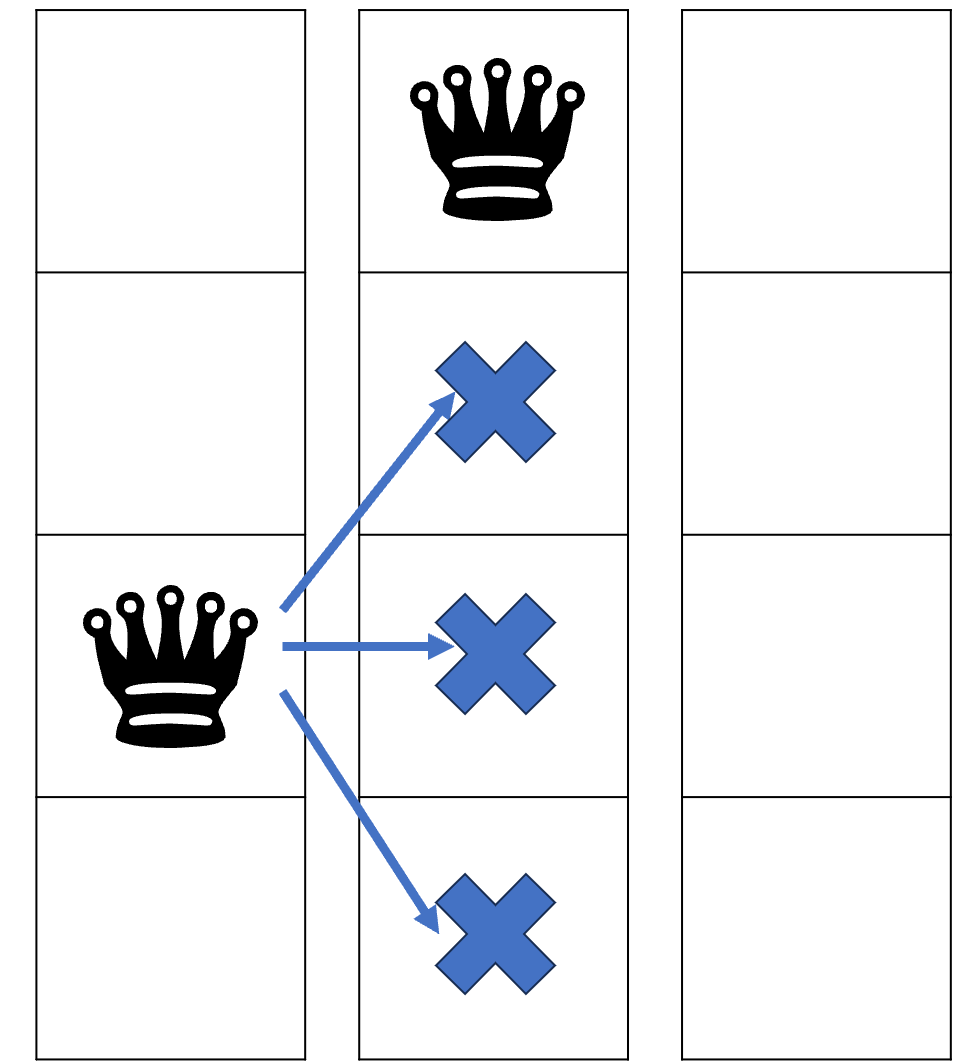
물론 이해한다고 바로 응용할 수 있는 것도 아니지만 프로그래밍에 대한 시각이 더 넓어진 느낌이다. 더욱더 공부해야겠다.
'기록 > 알고리즘' 카테고리의 다른 글
| 알고리즘 - 누적합 (0) | 2024.11.14 |
|---|---|
| 알고리즘 - 동적프로그래밍 Dynamic Programming (0) | 2024.11.13 |
| 알고리즘 - DFS와 BFS (1) | 2024.10.22 |
| 알고리즘(17) - NP-완비 (0) | 2023.06.09 |
| 알고리즘(16) - 문자열 매칭 (0) | 2023.06.08 |