집합의 처리
여기서 다루는 집합은 상호배타적 집합 disjoint set뿐이므로 교집합 연산은 다루지 않는다.
상호배타적 집합을 다루기 위해 필요한 연산은 다음과 같다.
makeSet(x) : 원소 x로만 이뤄진 집합을 생성한다.
findSet(x) : 원소 x가 속한 집합을 알아낸다.
union(x, y) : x와 y가 속한 집합의 합집합을 구한다.
집합의 연산은 위와 같다. 다음은 위 집합의 처리를 할 때 가장 근본적으로 고려해야 할 집합의 구현방법이다.
- 연결리스트로 구현 : makeSet, findSet은 O(1), union은 O(log n)이 소요된다.
- tree로 구현 : makeSet, findSet, union에서 O(m)의 시간이 소요된다. 가장 효율적이다.
연결리스트로 집합 처리
각 원소를 하나의 노드로 만들고, 그 노드가 속한 집합을 하나의 연결리스트로 관리한다.
집합의 대표원소는 맨 앞의 원소이며, union 연산을 위해 마지막 원소를 가리키는 변수 tail을 둔다.
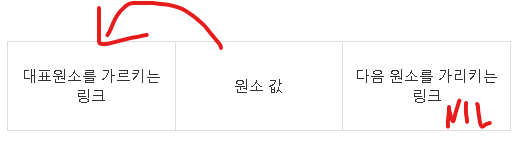
- makeSet : 노드를 하나 만들어 원소 x를 저장하고, 첫 원소일 때는 대표원소 링크를 자기자신에게 가리키도록 한다. 당연히 다음 원소는 없으므로 NIL. 기존 집합에 추가할 때는 앞의 링크를 대표원소를 가리키도록 하고 뒤의 링크는 다음 원소를 가르키도록 한다.
- findSet : 원소 x가 속한 집합을 알아낼 수 있다. 집합 = {a, b, c} 에서 어느 원소를 findSet 연산해도 대표원소는 a이다.
- union(c, g) : 각각을 수행하여 대표원소를 알아낸 후, 한 집합을 다른 집합의 뒤에 붙인다. A={a,b} , B={v,c,f}라면 {v,c,f,a,b}나 {a,b,v,c,f}가 된다.
여기서 알아둬야 할 점이 있다. 연결리스트에서 union 연산을 할 때는 무게를 고려해서 큰 집합 뒤에 작은 집합을 붙일 수 있다. 이로써 대표원소를 가리키는 링크 갱신 작업을 최소화할 수 있다.
트리로 집합 처리
일반적인 트리와 그 구조는 같지만 집합을 처리할 때는 자식 노드가 부모노드를 가리키도록 해야 한다. 하나의 트리의 대표원소는 루트노드이다.

- makeSet : 연결리스트와 같이 원소가 하나일 때는 링크가 자신을 가리키도록 한다.
- findSet : 원소 x가 속한 집합을 알아낼 수 있다. 집합 = {a, b, c} 에서 어느 원소를 findSet 연산해도 대표원소는 a이다.
- union(c, g) : 각각을 수행하여 대표원소를 알아낸 후, 한 집합을 다른 집합의 루트노드에 붙인다. A={a,b,c,h} , B={d,e,f,g}라면 다음과 같다.

집합처리 알고리즘은 다음과 같다. makeSet은 제외하겠다.
int findSet(x){ //원소가 정수값이란 가정하에
if(x == x.parent){
return x;}
else {
return findSet(x.parent);}
}
int union(x,y){
findSet(y).parent = findSet(x);}
트리 집합의 연산 효율 높이는 법
트리의 집합 처리에 있어서 다음과 같은 방법으로 연산의 효율을 높일 수 있다.
- 랭크를 이용한 union : union 연산을 수행하여 트리가 확장될 때 트리 높이를 가능한 낮게 유지할 수 있도록 한다.
- 랭크 rank : 각 노드에 랭크라는 이름의 필드를 두고, 자신을 루트로 하는 서브트리의 높이를 저장한다. 자식 노드가 없다면 서브트리의 높이는 0이다. 루트노드의 랭크가 그 집합의 랭크다.
- union 연산 시에 랭크가 낮은 집합을 랭크가 높은 집합에 붙인다.
- 경로압축 path compression : findset 연산을 수행하는 과정에서 만나는 모든 노드에 대해 직접 루트노드를 가리키도록 포인터를 변경하여 경로 길이를 줄인다.
랭크를 이용한 알고리즘 구현은 다음과 같다.
Union(x, y)
{
x' ← Find-Set(x);
y' ← Find-Set(y);
if (x'.rank > y'.rank) // y랭크가 x랭크보다 작다면
then y'.parent ← x' ;
else {
x'.parent ← y' ;
if (x'.rank = y'.rank) then y'.rank ← y'.rank + 1;
}
}경로압축을 이용한 알고리즘은 다음과 같다.
Find-Set(x)
{
if (x.parent ≠ x) then ▷ x가 대표 원소(루트 노드)가 아니면
x.parent ← Find-Set(x.parent); ▷ x의 parent의 대표 원소를 찾아 x의 parent로 삼음
return x.parent;
}
728x90
반응형
'기록 > 알고리즘' 카테고리의 다른 글
| 알고리즘(14) - 그래프 (0) | 2023.05.24 |
|---|---|
| 알고리즘(13) - 동적 프로그래밍 dynamic programming (0) | 2023.05.17 |
| 알고리즘(11) - 해시테이블 Hash table (0) | 2023.04.18 |
| 알고리즘(10) - 검색트리 - B-Tree, 다차원 검색트리(KD-Tree) (0) | 2023.04.06 |
| 알고리즘(9) - 검색트리 - 레드블랙트리 red-black tree (0) | 2023.04.04 |