동적 프로그래밍
큰 문제에는 닮은 꼴의 작은 문제가 깃들기도 한다. 이를 해결한 것이 재귀적 알고리즘인데, 이 알고리즘은 잘 쓰면 효율적인 보약이지만 잘못 쓰면 치명적인 맹독이다.
재귀적 알고리즘 자체가 심한 중복 호출을 불러올 수 있기 때문이다.
이를 해결하기 위한 방법이 동적 프로그래밍이다.
심한 중복 호출이 일어나는 경우는 피보나치 수열과 행렬곱셈 최적순서 구하기가 있다. 이에 대해 알아보자.
피보나치 수 구하기
피보나치 수열의 정의는 다음과 같다.
f(n) = f(n-1) + f(n-2)
f(1) = f(2) = 1
이를 프로그램으로 구현하면
fib(n)
{
if (n = 1 or n = 2)
then return 1;
else return (fib(n-1) +fib(n-2));
}여기서 수가 커질수록 엄청난 중복호출이 일어난다.
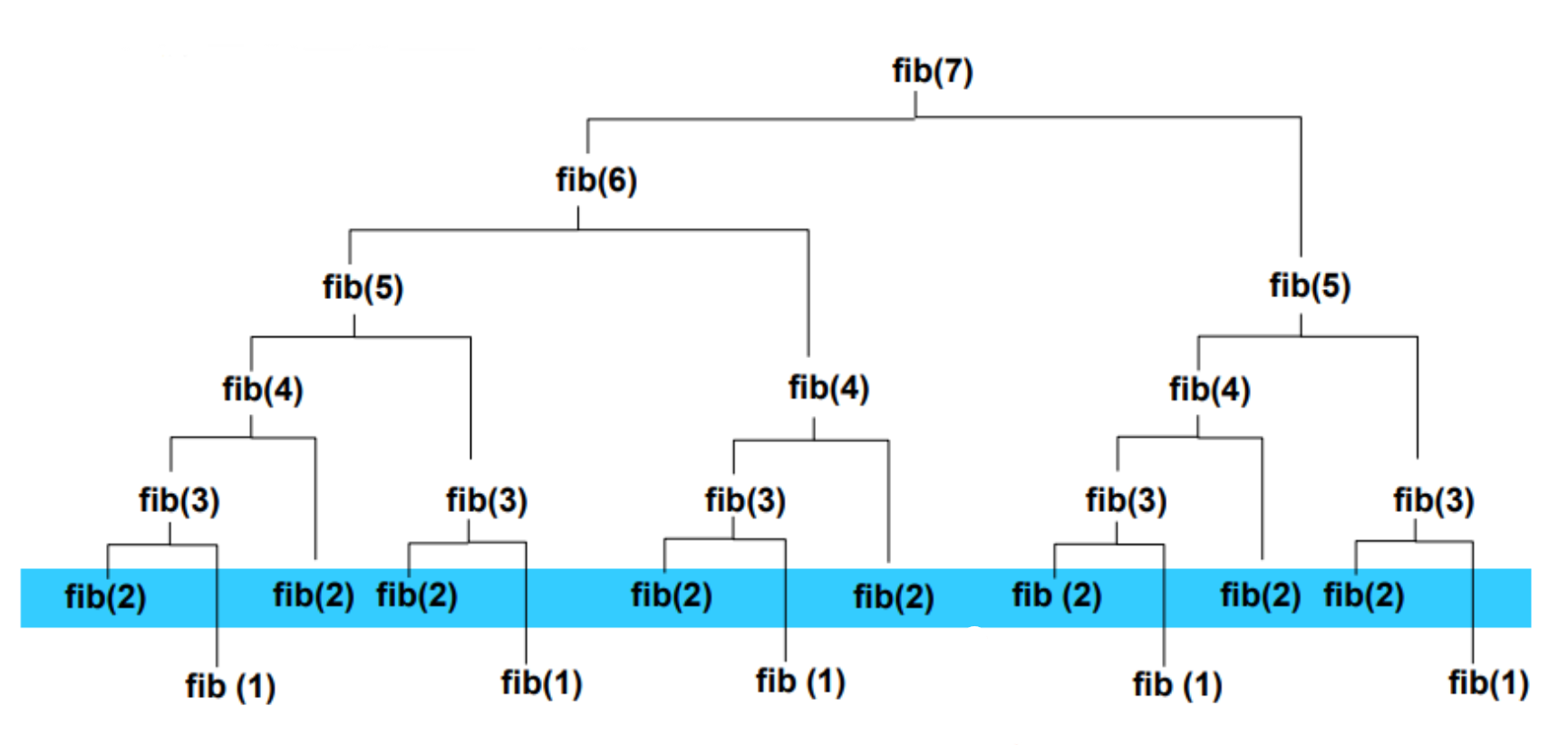
다음은 재귀적 알고리즘이지만 중복호출이 일어나지 않는 구현이다.
factorial(n)
{
if (n=1) return 1 ;
return n * factorial(n-1) ;
}
앞선 위의 알고리즘에서 중복호출을 예방하려면 호출 결과를 처음 얻었을 때 저장해 두고 필요할 때 사용 하면 된다. 동적 프로그래밍의 핵심은 부분 결과를 저장하면서 해를 구해 나가는 것이다.
동적 프로그래밍 알고리즘에는 두 가지 종류가 있다.
Top-down 방식
- 재귀적으로 구현하되, 호출된 적이 있으면 배열 f[ ]에 메모 해 두어(memoization = 메모리에 저장) 중복 호출 문제 해결한다. 배열 f[ ]의 원소는 0으로 초기화된다. f[i]의 값이 0이면 fib(i)가 아직 한 번도 수행되지 않았음을 의미한다.
fib(n)
{
if (f[n] ≠ 0) then return f[n]; ▷ 호출된 적이 있으면
else {
if (n = 1 or n = 2)
then f[n] ← 1;
else f[n] ← fib(n-1) + fib(n-2);
return f[n];
}
}
Bottom-up 방식
- 작은 문제의 해부터 테이블에 저장해가면서 이들을 이용해 큰 문제들의 해를 구해 나간다. 더 흔히 사용되는 방식이다.
fibonacci(n)
{
f[1] ← 1;
f[2] ← 1;
for i ← 3 to n
f[i] ← f[i-1] + f[i-2];
return f[n];
}
동적 프로그래밍의 적용 요건
- 최적 부분구조(optimal substructure) – 큰 문제의 최적 솔루션에 작은 문제의 최적 솔루션이 포함됨.
- 재귀 호출시 중복(overlapping recursive calls) – 재귀적 해법으로 풀면 같은 문제에 대한 재귀 호출이 심하게 중복됨.
이 두 가지가 모두 해당되면 동적 프로그래밍이 해결책이다.
행렬 경로 문제
행렬 경로 문제는 구성된 n×n 행렬 이 주어지고, 행렬의 좌상단에서 시작하여 우하단까지 이동한다. 여기서 목표는 무조건 우측과 하단으로만 움직일 수 있고, 방문한 칸에 있는 수들을 더한 값이 최대가 되도록 한다는 것이다.

행렬 경로 문제도 재귀적으로 처리했을 때 지나친 중복 문제가 발생한다. 따라서 동적 프로그래밍 알고리즘이 필요하다.
matrixPath(n){
for i ← 0 to n
c[i, 0] ← 0;
for j ← 1 to n
c[0, j] ← 0;
for i ← 1 to n
for j ← 1 to n
c[i, j] ← mij + max(c[i-1, j], c[i, j-1]);
return c[n, n];
}위와 같이 동적 프로그래밍을 활용하여 부분문제의 답을 배열에 저장하고 사용한다.
시간복잡도는 Θ(n^2)이다.
최장 공통 부분순서 LCS
두 문자열에 공통적으로 들어간 공통 부분 순서 중 가장 긴 것을 찾는 것이다. LCS는 Common subsequence 중에서 가장 긴 것을 고른다.
두 문자열에서 부분순서라 함은, 순서가 지켜진 공통 문자열을 의미한다.
예 : <abcbd>와 <abccd>의 <abd>
기본적으로, 이를 재귀 알고리즘으로 해결했을 땐 중복문제가 일어나지만 동적 프로그래밍을 사용하여 해결할 수 있다. 코드는 다음과 같다.
LCS(m, n)
{
for i ← 0 to m
C[i, 0] ← 0;
for j ← 0 to n
C[0, j] ← 0;
for i ← 1 to m
for j ← 1 to n
if (xi= yj)
then C[i, j] ← C[i-1, j-1] + 1;
else C[i, j] ← max(C[i-1, j], C[i, j-1]);
return C[m, n];
}
위의 코드를 이해하기 위해 그림으로 보여주자면 다음과 같다.
X₄ = baba
Y₃ = aab

시간 복잡도는 Θ(mn)이다.
'기록 > 알고리즘' 카테고리의 다른 글
| 알고리즘(15) - 그리디 알고리즘 greedy algorithm (0) | 2023.06.07 |
|---|---|
| 알고리즘(14) - 그래프 (0) | 2023.05.24 |
| 알고리즘(12) - 집합의 처리 (4) | 2023.05.08 |
| 알고리즘(11) - 해시테이블 Hash table (0) | 2023.04.18 |
| 알고리즘(10) - 검색트리 - B-Tree, 다차원 검색트리(KD-Tree) (0) | 2023.04.06 |