점화식 Recurrence relation
어떤 함수를 자신보다 더 작은 변수에 대한 동일 함수와의 관계로 표현한 것!
사전적 의미는 이렇다. 당연히 잘 이해가 되지 않는다. 풀어서 설명하면 다음과 같다.
-> 동일한 함수가 등호나 부등호 양쪽에 나타난다. 이 두 함수의 변수 크기는 다르다. 하지만 동일하다.

입력 크기가 작으면 알고리즘의 효율성을 굳이 따질 필요가 없다. 허나 크기가 커지면 얘기가 다르다. 이런 경우를 위한 분석이 '점근적 분석 Asymptotic analysis'이다.
이번에는 점화식으로 표현한 재귀 알고리즘을 점근적 표기로 나타내는 방법을 알자.
재귀 알고리즘의 수행시간 ->점화식으로 표현
재귀로 표현한 병합정렬을 보자.
mergeSort(A[ ], p, r) ▷ A[p ... r]을 정렬한다.
{
if (p < r) then {
q ← (p+r)/2; ----------- ① ▷ p, r의 중간 지점 계산
mergeSort(A, p, q); ------- ② ▷ 전반부 정렬
mergeSort(A, q+1, r); ------ ③ ▷ 후반부 정렬
merge(A, p, q, r); -------- ④ ▷ 병합
}
}
merge(A[ ], p, q, r)
{
정렬되어 있는 두 배열 A[p ... q]와 A[q+1 ... r]을 병합하여
정렬된 하나의 배열 A[p ... r]을 만든다.
}주어진 배열에서 반을 자른다고 이해해보자. 입력크기가 n일 때, 2번의 전반부 정렬의 수행시간은 T(n/2)다. 3번 후반부 정렬도 마찬가지다.
따라서 입력크기 n의 병합정렬 수행시간을 점화식으로 표현하면,
점화식 : T(n) = 2T(n/2) + 오버헤드
점화식의 점근적 분석
그렇다면 위의 점화식에서 어떻게 점근적 복잡도 도출해낼까?
방법은 다음 세 가지다.
- 반복대치 repeated substitution : 더 작은 문제에 대한 함수로 반복해서 대치해 나가는 해법
- 추정 후 증명 guess and vertification : 결론을 추정하고 수학적 귀납적으로 증명하는 해법
- 마스터 정리 master theorem : 점화식이 T(n) = aT(n/b) + f(n)로 주어진 경우, 바로 복잡도를 구하는 법
반복대치 repeated substitution
반복대치의 예를 들어보자.

팩토리얼을 구하는 알고리즘을 점화식으로 표현하면,

위와 같이 된다. T(1)은 c보다 작거나 같다. 이를 이용하면,

T(n)은 n보다 작거나 같다. 따라서 O(n)으로 표현할 수 있다.
추정 후 증명 guess and verification
한 문제에 대해 경계조건에서 성립하는지를 먼저 확인 후, 귀납 가정에서도 성립하는지 증명하는 것이다.
T(n) = 2T(n/2) + n
위의 점화식에서의 점근적 표기를 T(n) = O(n log n) 이라고 하자. 충분히 큰 n에 대해 T(n) ≤ cn log n인 양의 상수가 존재한다고 추정한다.
그렇다면,
- 경계 조건 : 2에 대해 성립, T(2) ≤ c2 log 2 인 c가 존재
- 귀납 가정 : n/2에 대해 성립, T(n/2) ≤ c(n/2) log (n/2)

->T(n) ≤ cn log n를 만족하는 상수 c가 존재하기에 T(n) = O(n log n)은 성립한다.
마스터 정리 master theorem
점화식이 T(n) = aT(n/b) + f(n) (단, a≥1, b>1) 의 형태를 갖췄다면 마스터 정리에 의해 바로 점근적 복잡도를 알아낼 수 있다.
T(n) = aT(n/b) + f(n) (단, a≥1, b>1)이 의미하는 바는 다음과 같다.
크기 n인 문제를 푸는 시간 = 크기 n/b인 문제 a개를 푸는 시간+나머지 오버헤드 f(n)
또한 a≥1, b>1 에 대해, 점화식 T(n) = aT(n/b) + f(n) 에서 n^logb a = h(n)이라 하면 T(n)의 개략적인 점근적 복잡도는 다음과 같다.
① lim 𝑛→∞ 𝑓(𝑛) ℎ(𝑛) = 0 이면 T(n) = Θ(h(n))이다.
② lim 𝑛→∞ 𝑓(𝑛) ℎ(𝑛) = ∞ 이고, 충분히 큰 모든 n에 대해 af( 𝑛/ 𝑏 ) < f(n) 이면 T(n) = Θ(f(n))이다.
③ f(n)/h(n) = Θ(1)이면 T(n) = Θ(h(n) log n)이다.
이는 곧, 아래를 의미한다.
① h(n)이 더 무거우면 h(n)이 수행시간을 결정한다.
② f(n)이 더 무거우면 f(n)이 수행시간을 결정한다.
③ h(n)과 f(n)이 같은 무게이면 h(n)에 log n을 곱한 것이 수행시간이 된다.
이제 바로 예시를 풀어보자.
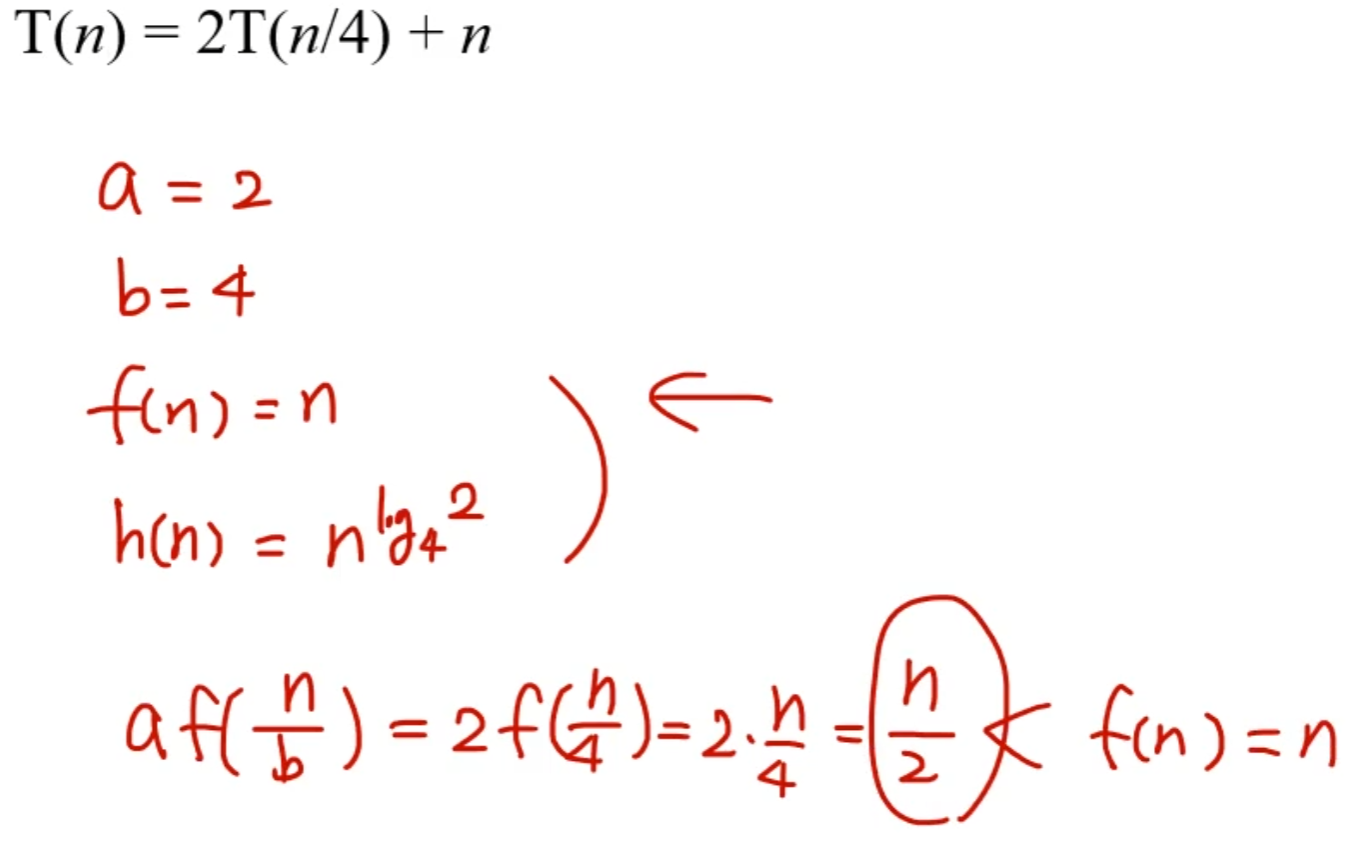
f(n)이 더 무거우므로, 수행시간은 f(n)이 정한다. 따라서, T(n)=Θ(n)이다.
'기록 > 알고리즘' 카테고리의 다른 글
| 알고리즘(5) - 정렬(고급 정렬) (1) | 2023.03.22 |
|---|---|
| 알고리즘(4) - 정렬 (기본적인 정렬) (0) | 2023.03.14 |
| 알고리즘(2) - 알고리즘 설계와 기초 분석 (1) | 2023.03.08 |
| 알고리즘(1) - 알고리즘이란 (1) | 2023.03.08 |
| 검색 알고리즘 (1) | 2022.12.06 |