기록하는 습관 "기습"

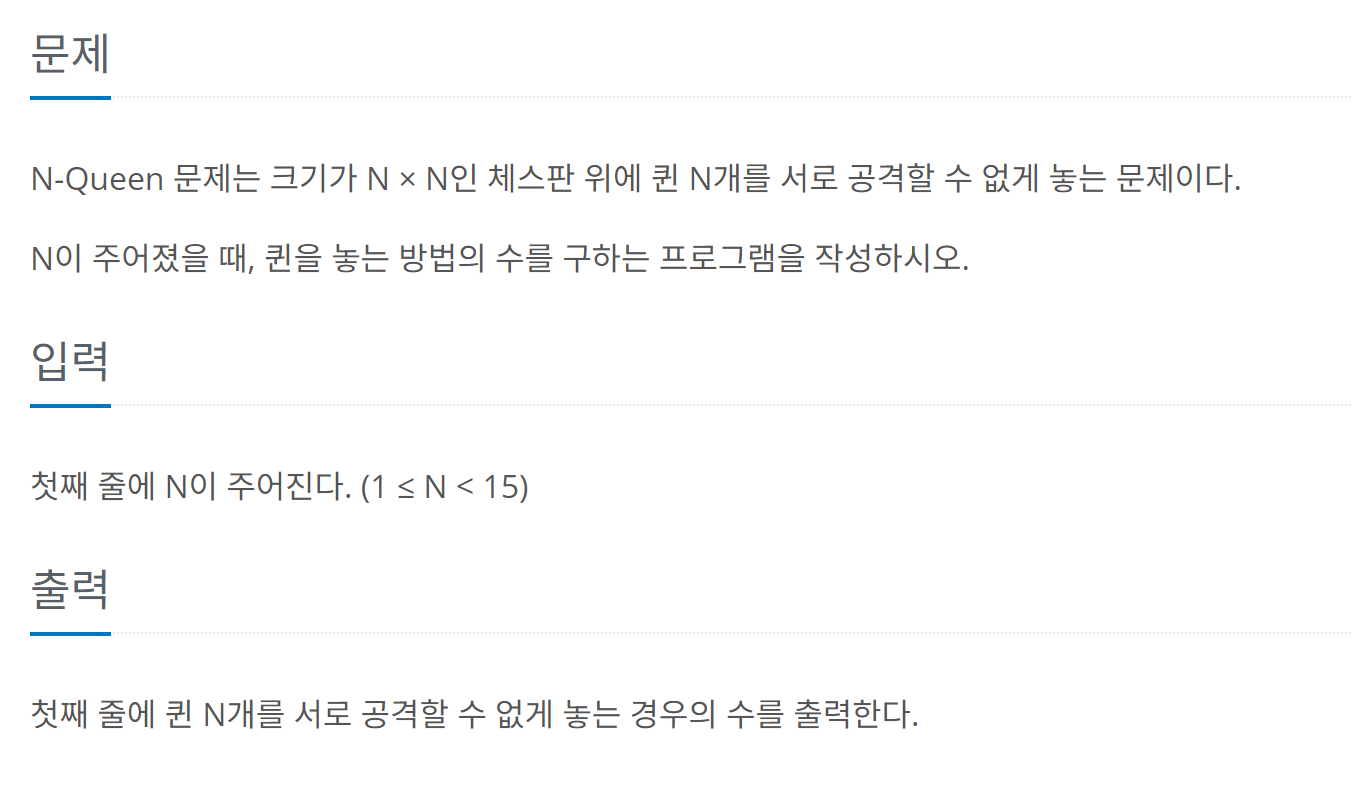
백트래킹이란?백트래킹은 해를 찾는 과정에서 여러 가능성을 탐색하다가, 특정 경로가 잘못되었음을 알게 되면 되돌아가서 다른 경로를 시도하는 문제 해결 기법이다. 모든 가능한 경우의 수를 탐색하지만, 가지치기(pruning)를 통해 비효율적인 경로를 배제하여 효율성을 높인다. 다시 말해, 완전 탐색(브루트 포스)의 개선된 형태라 할 수 있다. 단순히 요약하자면, 백트래킹은 "이 길이 아닌 것 같을 때 원래 왔던 길로 되돌아가서 다른 길을 가보는 것"이다. 이는 특성으로 알 수 있듯이 대부분 DFS로 구현할 수 있다.  백트래킹의 예시이번 예시는 9663번 N-Queen 문제를 기준으로 하겠다. 먼저 구현 문제를 보자.  문제 자체는 백트래킹을 잘 활용해야 풀 수 있다. 나는 문제를 다 읽고 2차원 배열로 풀..

개요코테 준비를 시작했는데 너무 부족함을 느끼고 있다. 나오는 문제는 막힘없이 풀 수 있는 정도가 되고 싶다. 왜 이렇게 해야 하는가에 대한 이유는 다음 글을 읽어보길 바란다. 도움이 되는 내용도 많다! https://yozm.wishket.com/magazine/detail/2755/ 개발자를 위한 실전 ‘코딩테스트’ 준비 팁 | 요즘IT개발자라면 누구나 ‘코딩테스트’를 준비해 본 경험이 있을 겁니다. 코딩테스트는 여러분의 두뇌가 얼마나 비상한지, 복잡하게 꼬인 문제를 얼마나 천재적인 발상으로 해결할 수 있는지 시험yozm.wishket.com 그래서 나는 이전에 강의로 배웠던 내용을 다시 공부하거나 부족한 부분을 채우려고 한다. 처음은 DFS와 BFS로 스타트를 끊고자 한다. 설명은 백준의 1260번..

NP 완비 NP-complete 요약하자면, 현실적인 시간 내에 답을 얻을 수 있는 해법이 존재하는 것을 말한다. 여기서 이제까지 다룬 모든 알고리즘은 다항식 시간, 즉 입력 크기가 n일 때 최악의 경우에도 수행시간이 O(n^k)의 시간이 걸리는 알고리즘들이었다. 하지만 모든 문제를 컴퓨터로 다항식 시간에 풀 수 있지 않다. 정확히는 풀 수 있으나 현실적인 시간 내에 풀 수 없는 문제가 있고, 아무리 시간이 주어져도 풀 수 없는 문제가 존재한다. 간혹 들어보는 표현 중에 "슈퍼 컴퓨터로 몇 십년 이상 걸리는 문제"가 그것이다. P 는 polynomial이란 의미로, 문제가 주어졌을 때, 대답을 다항식 시간에 할 수 있는 문제이다. NP는 yes라는 근거만 주어지면 다항식 시간에 풀 수 있는 문제이다. N..

원시적인 naive 매칭 문자열 하나하나에 패턴문자열을 대조해보는 방법으로, O(mn)의 수행시간을 갖는다. 다만 이전에 비교했던 불일치 건에 대한 사실을 전혀 활용하지 못하기에 비효율적이다. Rabin-Karp 알고리즘 문자열 패턴을 수치화하여 문자열 비교를 수치비교로 대신한다. 수치화 방법은 다음과 같다. 가능한 문자 집합의 크기에 따라 진수가 결정된다. 만약 A = {a,b,c,d,e}이면, |A| = 5이다. 여기서 문자열 ad를 수치화한다고 했을 때 수치는 다음과 같다. 0*5^1 + 3*5^0 = 4 (4가 문자열 ad의 수치화, 맨앞의 숫자는 알파벳의 순서) 문자열 수치화로 문자열 매칭을 수행하려면 다음과 같은 문제점을 해결해야 한다. 수치화 작업의 부담 보통 하나의 문자열들을 일일이 계산하..

그리디 알고리즘 눈앞의 이익만 우선 추구하는 알고리즘을 총칭한다. 최적해를 찾을 수 있으면 찾지만, 없다면 그런대로 괜찮은 해를 찾아내는 것이 목표다. 이 때문에 대부분 최적해를 보장하지 못하지만 드물게 최적해를 보장하는 경우도 있다. 그리디 알고리즘으로 최적해가 보장되는 않는 예는 다음과 같다. 이진트리 최적합 경로 찾기 동전 바꾸기 배낭 문제 최적해가 보장되는 예는 다음과 같다. 최소 신장 트리 : prim, kruskal 최단 경로 : 다익스트라 회의실 배정 문제 여기서 몇가지를 뽑아서 설명하겠다. 동전 바꾸기 동전을 모아서 특정 액수를 만들되 동전의 개수를 최소로 하는 문제다. 다만 이 문제는 모든 동전의 액면이 일반적인 화폐의 유통과 같았을 때, 즉 500원, 100원, 50원, 10원일 때 그..

그래프는 정점 vertex와 간선 edge로 사물과 현상을 표현한 것이다. 이전에 다뤘기에 세세한 것은 넘어가겠다. 그래프의 표현 그래프를 표현하는 방법 중에는 인접 행렬, 인접 리스트, 인접 배열, 인접 해시테이블이 있다. 인접행렬은 간선 수 이상의 공간을 차지하고, 인접리스트는 특정 간선 존재 여부를 검사하는 데에 오래 걸린다. 이 두 단점을 커버할 수 있는 표현은 인접 배열이다. 인접배열은 정점 N개일 때 N개의 인접배열로 표현하는 것이다. 즉, 인접한 정점의 갯수만큼 배열을 또 생성한다. 인접리스트를 배열로 표현한다면 이해가 쉬울 것이다. 이때 간선 존재 여부의 수행시간은 O(log k)이다. 인접 해시테이블은 각 정점마다 인접배열을 두는 대신 하나의 해시 테이블을 사용하는 것이다. 인접한 정점이..

동적 프로그래밍 큰 문제에는 닮은 꼴의 작은 문제가 깃들기도 한다. 이를 해결한 것이 재귀적 알고리즘인데, 이 알고리즘은 잘 쓰면 효율적인 보약이지만 잘못 쓰면 치명적인 맹독이다. 재귀적 알고리즘 자체가 심한 중복 호출을 불러올 수 있기 때문이다. 이를 해결하기 위한 방법이 동적 프로그래밍이다. 심한 중복 호출이 일어나는 경우는 피보나치 수열과 행렬곱셈 최적순서 구하기가 있다. 이에 대해 알아보자. 피보나치 수 구하기 피보나치 수열의 정의는 다음과 같다. f(n) = f(n-1) + f(n-2) f(1) = f(2) = 1 이를 프로그램으로 구현하면 fib(n) { if (n = 1 or n = 2) then return 1; else return (fib(n-1) +fib(n-2)); } 여기서 수가 ..

집합의 처리 여기서 다루는 집합은 상호배타적 집합 disjoint set뿐이므로 교집합 연산은 다루지 않는다. 상호배타적 집합을 다루기 위해 필요한 연산은 다음과 같다. makeSet(x) : 원소 x로만 이뤄진 집합을 생성한다. findSet(x) : 원소 x가 속한 집합을 알아낸다. union(x, y) : x와 y가 속한 집합의 합집합을 구한다. 집합의 연산은 위와 같다. 다음은 위 집합의 처리를 할 때 가장 근본적으로 고려해야 할 집합의 구현방법이다. 연결리스트로 구현 : makeSet, findSet은 O(1), union은 O(log n)이 소요된다. tree로 구현 : makeSet, findSet, union에서 O(m)의 시간이 소요된다. 가장 효율적이다. 연결리스트로 집합 처리 각 원소..

해시테이블  지금까지 트리 자료구조는 대부분은 다른 원소와 비교하여 저장할 위치를 찾아갔다. 그러나 해시테이블은, 원소를 저장할 위치가 그 원소 값에 의해 결정되는 자료구조다. 해시테이블의 특징은 다음과 같다. 저장/검색/삭제에 있어서 상수에 가까운 수행시간을 갖는다. = > Θ(1)최소 원소 찾기 같은 연산은 지원하지 않는다. 지금부터 위의 그림을 예시로 해시테이블에 대해 설명하겠다.위와 같은 해시테이블의 크기 m을 7이라 하자. 그렇다면 테이블은 0~6까지의 인덱스를 갖는다. 해시함수 Hash function원소를 저장할 때, 가운데 해시함수 hash function를 거쳐서 적절한 위치에 저장된다. 따라서 해시함수는 검색 키 값을 해시 테이블주소로 매핑하는 함수라는 의미다.  해시함수는 입력원소가 ..

B-Tree 검색트리가 방대하면 모두 메모리에 올려놓고 사용할 수 없다. 따라서 디스크에 넣어둔 상태로 작업해야 한다. 이는, 외부 검색트리에 해당한다. 외부검색트리일 땐 CPU보다는 디스크 접근 횟수가 효율을 좌우한다. 그리고 트리의 높이를 최소화하는 것이 유리하다. 이는 분기수를 늘리면 다진 검색트리가 되고 높이도 줄어든다. 10억 개의 키값을 가진 이진검색트리는 높이가 30이다. 256개의 분기를 가진 트리는 5의 높이를 갖는다. 이러한 분기는 블럭의 크기를 고려하여 결정한다. B-Tree는 결국 트리 균형을 유지하여 최악의 경우 디스크 접근 횟수를 줄인다. 또한, 다진검색트리로써 다음과 같은 특성을 갖는다. 루트노드를 제외한 모든 노드에서 [k/2]~k개의 키를 갖는다. 모든 리프 노드는 똑같은 ..