기업
기업은 생산활동에 전문화를 추구하며 결과적으로 이윤극대화를 목표로 한다.
생산에 투입되는 요소는 시간경과에 따른 투입량의 변화 가능여부와 기간에 따른 구분으로 나뉜다.
투입량이 변화할 수 있으면 가변투입요소
투입량이 변화하지 않으면 고정투입요소
기준이 있지 않지만 보통 고정투입요소가 있으면 단기, 없으면 장기로 친다.
생산함수
주어진 시간동안 여러가지 생산요소의 양과 이를 통해 그 기간동안 생산할 수 있는 최대 상품량 사이의 관계를 생산함수라고 한다.
Q = f(L, K , R)
L은 노동투입량, K는 자본투입량, R은 원자재사용량이다.
만약 노동과 자본 두 생산요소만 사용된다고 가정하면 생산함수는 Q = f(L, K)로 표현될 수 있다.
총생산, 한계생산 그리고 평균생산
일정기간 동안 자본을 투입한다고 가정하자. 이는 k'라 표현한다. 이때 노동 투입량만 계속 증가시킨다. 이렇게 되면 그 기간 동안 투입된 노동의 양에 대해 같은 기간 동안 최대한으로 생산할 수 있는 하나의 산출수준이 대응하게 된다. 그 관계에 대한 표현을 다음과 같다.
Q = f(L, k')
이 함수관계를 아래와 같은 그림으로 옮겼다.
아래 그림을 분석하며 총생산, 한계생산, 평균생산에 대해 알아볼 것이다.
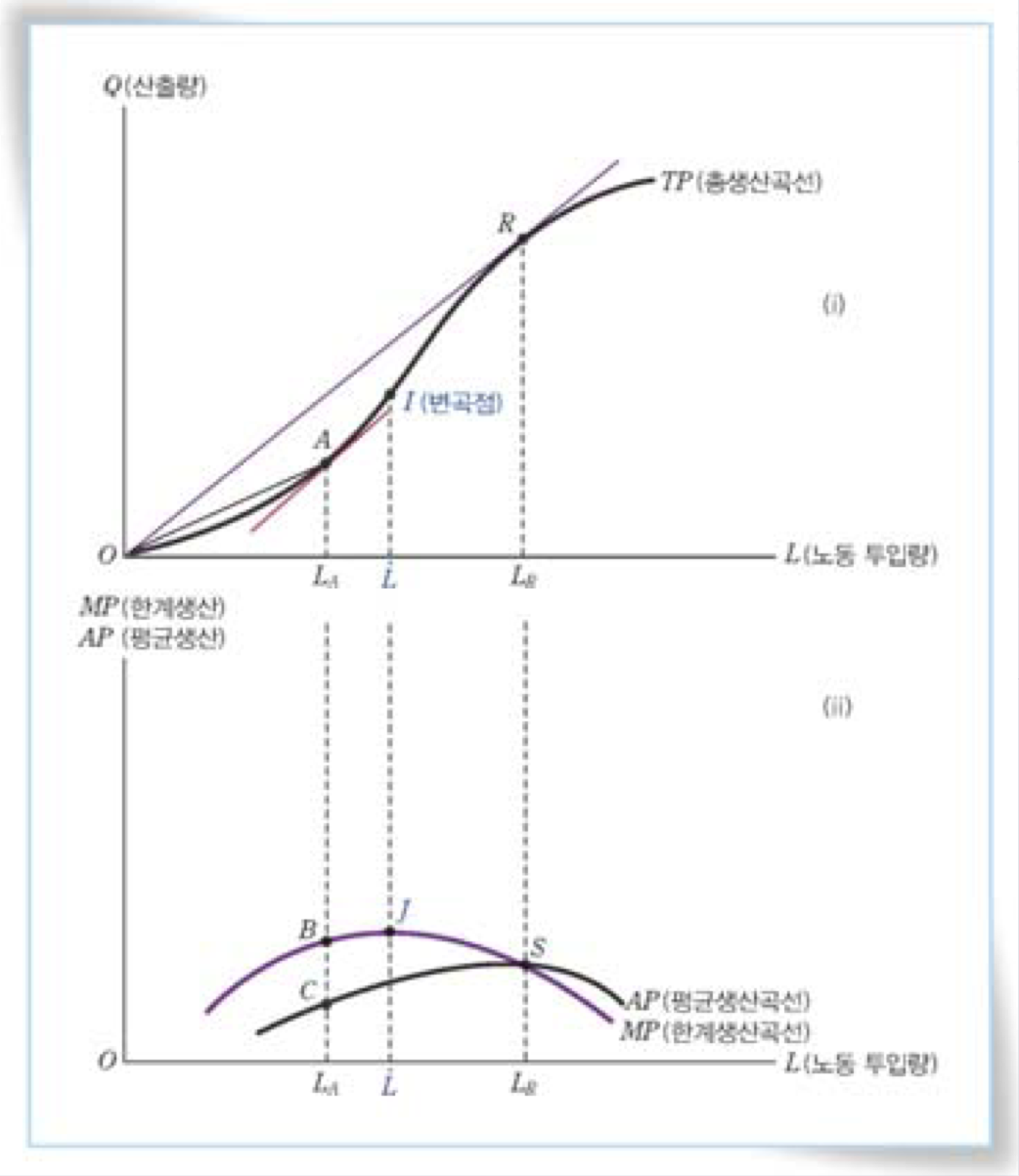
TP곡선이 총생산곡선이다.
TP곡선만 보자면 변곡점을 기준으로 왼쪽은 노동투입량을 늘려감에 따라 생산량이 가파르게 증가하지만 변곡점의 오른쪽으로 갈수록 생산량이 둔화됨을 볼 수 있다.
한계생산은 다른 생산요소를 묶어둔 채 가변투입요소만을 1증가시켰을 때 산출량의 증가분이다. 한계생산은 MPL로 표현할 수 있고, 다음 식으로 표현할 수 있다.
MPL = 산출량의 변화 / 노동투입량의 변화 = ΔQ / ΔL
한계생산을 위 그림으로 표현할 때는 한계생산곡선 MP곡선이라 한다.
J점까지 우상향하다가 J점을 지나고부터 우하향하는 모습을 보인다.
평균생산은 투입된 생산요소 1단위당 산출량을 뜻한다. 산출량을 요소투입량으로 나누면 된다.
APL = 산출량 / 요소투입량 = Q / L
평균생산곡선을 잘 보면 평균생산이 최대가 되는 점에서 한계생산곡선과 만난다.
또 한 가지, 위 그림을 통해 알아야 할 것이 있다. MP곡선을 보면 J점을 지나면서 한계생산이 점차 감소한다는 것을 알 수 있다. 이를 현상을 "한계생산체감의 법칙"이라고 한다.

여기서 한계생산 증가구간을 자르면 위와 같다.
이는, 다음과 같은 사실을 시사한다.
한계값 > 평균값 => 평균값 증가
한계값 = 평균값 => 평균값 일정(극대 혹은 극소 하는 지점)
한계값 < 평균값 => 평균값 감소
등량곡선
똑같은 수준의산출량을 가져다주는 생산요소 투입량의 조합들로 구성된 집합을 그림으로 나타낸 것.
등량곡선의 기본적 성격은 다음 다섯 가지다.
- 평면 상의 모든 점들은 그것을 지나는 하나의 등량곡선을 갖는다.
- 등량곡선은 우햐항하는 모양이다.
- 원점에서 더 멀리 떨어져있는 등량곡선일수록 더 높은 산출량을 대표한다.
- 두 등량곡선은 서로 교차할 수 없다.
- 등량곡선은 원점에 대해 볼록한 모양을 갖는다.
등량곡선의 성격들은 표준적인 생산기술의 특징을 대표한다. 무차별곡선의 경우와 흡사하지만 등량곡선은 구체적인 산출량의 수준과 연결된다. 이는 절대적으로 기수성을 중시한다는 의미다.

한계기술대체율
생산무차별지도를 보자. C에서 C'로 넘어가면 자본투입량이 ΔK만큼 감소하고 노동은 ΔL만큼 증가한다. 허나 이렇게 변해도 산출량에는 일절 변화가 없다. 이 교환비율을 한계기술대체율이라고 한다. 무차별곡선의 한계대체율과 같다.
RTS = - ( ΔK / ΔL ) = - 등량곡선의 기울기
등량곡선이 원점에 대해 볼록하다는 것은 한계기술대체율체감의 법칙이 성립함을 의미한다.
대체탄력성
생산요소 사이의 대체가능성을 나타낸다.
등량곡선이 평평한 모양을 가질수록 대체탄력성이 크다.
δ = 생산요소 투입비율의 변화율 / 한계기술대체율의 변화율 = ((ΔK/L)/ΔK/L)) / ΔRTS/RTS
극단적인 대체탄력성을 갖는 두 경우도 있다.
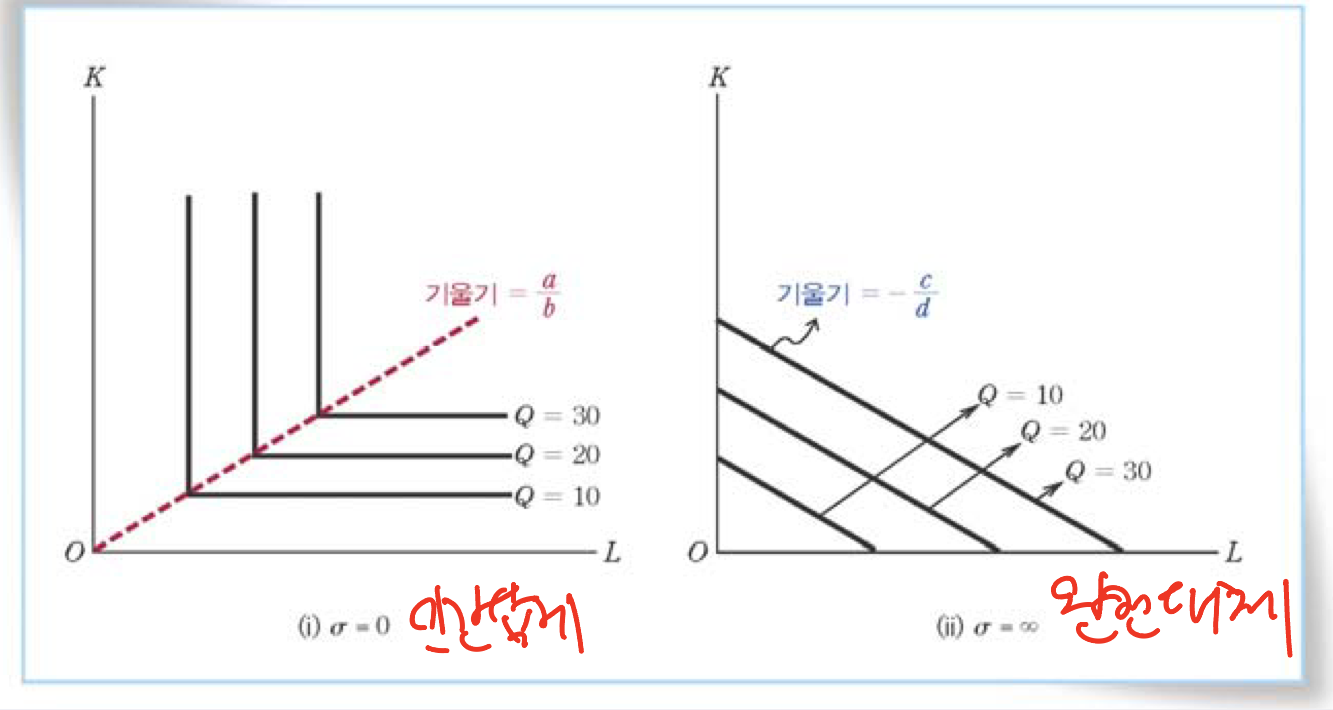
L모양의 등량곡선의 경우는 두 생산요소가 완전히 보완적인 관계일 때다. 이때는 대체탄력성이 0이다.
선분모양의 등량곡선은 두 생산요소가 완전히 대체적 관계일 때다. 이때 대체탄력성은 무한대다.
'기록 > 경제학' 카테고리의 다른 글
| 미시경제학(7) - 10장 (기업의 이윤극대화) (2) | 2023.04.17 |
|---|---|
| 미시경제학(6) - 생산자이론 ( 9장 생산비용 ) (2) | 2023.04.16 |
| 화폐와 금융 - 요약정리본(2장, 4장) (7) | 2023.04.12 |
| 미시경제학(4) - 소비자이론 (응용과 확장) (0) | 2023.04.05 |
| 미시경제학(3) - 소비자 이론 (수량지수) (2) | 2023.04.01 |